التأويلات الهندسية لنهايات الدوال – ملخص التأويل الهندسي للنهايات المعروفة – الدرس 3 –

نتابع التأويل الهندسي للنهايات في الرياضيات و هو تذكير مهم جدا في دراسة الدوال. لماذا؟ هذه التاويلات الهندسية لنهايات معروفة تظهر كثيرا في تمارين وطنيات الدوال. بحيث يطلب منك أولا حساب نهاية دالة مثلا، ثم يكون السؤال التالي، أعط تأويلا هندسيا لهذه النهاية. لذلك هي طريقة سهلة لكسب بعض النقط دون حساب كثير…

الفيديو الأول :

الدقيقة 00:00 : تتمة الفقرات التي سنتدرسها في التأويل الهندسي و التي تتمثل في :

التأويل الهندسي للنهايات : ثلاثة حالات مهمة

١-هناك أولا التأويل الهندسي للاشتقاق كما رأيناه في حساب النهايات هنا.

بحيث نحسب نهاية معدل التغير لإيجاد عدد مشتق، فنجد مثلا عدد أو زائد ما لا نهاية فنستنتج بعض الامور. انظر اسفله.

٢-التأويل الهندسي للنهايات دالة مثلا و الذي سنتعرف فيه على نهايات تعطي مقاربات و نهايات أخرى تعطي فروعا شلجمية.

٣-و في الأخير سنتعرف أيضا على تأويلات هندسية تتعلق بخاصيات عامة. مثل ماذا؟ مثل فردية الدالة و زوجية الدالة و أيضا تأويل الهندسي مهم بالنسبة للدالة العكسية.

التأويل الهندسي للنهايات معدل التغير

الدقيقة 01:47 :عندما نتحدث عن حساب نهاية الاشتقاق و خاصياته في نقطة x=a فنحن نكون أمام ثلاثة اختيارات ممكنة :

• يمكن أن نجد أن نهاية معدل التغير يعطينا عددا حقيقيا m.
• كما يمكن لهذه النهاية في نقطة أن تعطي ما لانهاية.
• الحل الاخر الممكن هو أن حساب هذه النهاية معدل التغير في نقطة أن تعطي ناقص مالانهاية.

الدقيقة 03:14 : ما هو التأويل الهندسي لحالة حساب الاشتقاق في نقطة و الحصول على m ينتمي الى R ؟ :

في هذه الحالة التأويل الهندسي الصحيح لهذه النهاية هو أن : Cf يقبل مماسا عند النقطة x= a بحيث المعامل الموجه لهذا المستقيم المماس هو m.

الدقيقة 05:24 : التأويل الهندسي لمماس الدالة f في نقطة معلومة.

لكن السؤال المطروح هو كيف يمكن أن نرسم هذا المماس في النقطة x=a؟

الجواب سهل. انطلاقا من النقطة a,f(a) نتقدم ب +1 حسب محور الافاصيل، ثم نصعد ب +m اذا كان m موجبا. أو ننزل ب -m اذا كان m سالبا.

التأويل الهندسي للاشتقاق في حالة زائد ما لا نهاية

الدقيقة 07:00 : نجد الحالة الثانية للتأويل الهندسي في حالة حساب الاشتقاق في نقطة عندما نحصل على نتيجة زائد مالانهاية.

ما هو التأويل الهندسي للاشتقاق في هذه الحالة؟

في هذه الحالة زائد ما لا نهاية، نقول أن منحنى الدالة Cf يقبل نصف مماس عند النقطة x=a و هو يكون موجها نحو الأعلى.

الدقيقة 8:00 : هنا نتعلم كيف نرسم المماس الموجه نحو الاعلى، و نضع التأويل الهندسي على منحنى الدالة مباشرة.

بالمناسبة، هذه مهارة يجب أن تتعلمها.

قد تبدو صعبة في البداية لكن اذا استوعبت جيدا هذه الحالات الثلاثة، سوف يسهل الامر عليك كثيرا.

التأويل الهندسي للاشتقاق في حالة ناقص ما لا نهاية

الدقيقة 09:00 : لنر الان الحالة الاخيرة للتأويل الهندسي للاشتقاق. أي حالة ناقص ما لا نهاية.

الامر بسيط. عندما يعطينا حساب النهاية ناقص ما لا نهاية، فآنذاك سوف نجد نصف مماس عند النقطة x=a و سوف يكون موجها نحو الاسفل.

الدقيقة 10:00: هذه هي الطريقة لكي نرسم المماس في حالة الحصول على ناقص ما لانهاية عند نقطة ؟.

في هذه الحالة يكون Cf يقبل نصف مماس عند x = a على شكل مستقيم موازي لمحور الاراتيب و موجه نحو الأسفل.

أنواع المقارب لمنحنى دالة Cf

الدقيقة 11:30 : ما هي أنواع المقاربات عند حساب النهايات ؟

أثناء حساب النهايات يمكن الحصول على ثلاث أنواع من المقاربات :

• مقارب أفقي.
• مقارب عمودي.
• مقارب مائل.

الدقيقة 12:21 : متى نحصل على مقارب أفقي و كيف يمكن تحديد معادلته و تمثيله ؟

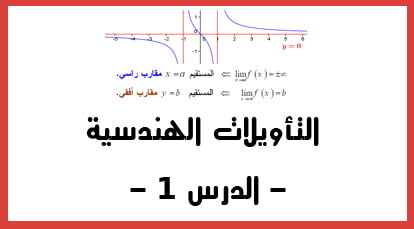
نحصل على مثل هذا المقارب عندما نجد حسابيا أن نهاية الدالة f عند زائد أو ناقص ما لا نهاية تساوي عدد حقيقي محدد b

Lim f(x)=b. en +oo ou -oo

الدقيقة 14:09 : متى نحصل على مقارب عمودي و كيف يمكن ان نجد معادلته و تمثيله ؟

نحصل على مقارب عمودي ل Cf عندما نحسب النهاية دالة في عدد محدد a. و نجد حسابيا أنها تساوي +oo. أو -oo

بمعنى آخر

oo = Lim (x->a)

الفيديو الثاني :

الدقيقة 00:00 : تتمة الشرح المتعلق بكيف يمكن رسم المقارب العمودي للدالة.

الدقيقة 00:38 : ما هو المقارب المائل و كيف يمكن تحديد معادلته و تمثيله المبياني ؟

الدقيقة 01:50 : مثال تطبيقي حول كيف يمكن رسم مقارب مائل معادلته y = 3x + 4 .

الدقيقة 05:28 : تلخيص لكل الفقرات المتعلقة بالمقاربات.

الدقيقة 06:35 : الانتقال الى الفقرة الثانية من من تحديد المقاربات  و هي المتعلقة بتحديد الفروع الشلجمية و التعرف على المراحل التي يجب اتباعها من أجل تحديد الفرع الشلجمي ’ حيث أننا في البدايىة نقوم بحساب النهاية عند ما لانهاية , مع الشرط الأول من أجل حساب الفرع الشرجمي هي أنه هذه النهاية لابد أن تعطي ما لانهاية و في الخطوة الموالية نقوم بحساب النهاية في مالانهاية ل f(x)/x , و في هذه الحالة يمكن أن نحصل على واحدة من هذه الاحتمالات  :

•  ما لا نهاية و في هذه الحالة Cf أي منحنى الدالة يقبل فرعا شلجميا اتجاهه محور الأراتيب.
• أو نحصب على 0 و في هه الحالة منحنى الدالة يقبل فرعا شلجميا اتجاهه محور الأفاصيل.
• عند الحصول على عدد حقيقي a و في هذه الحالة يجب حساب النهاية في مالانهاية ل f(x)-ax.

هل تجد مشاكل في تحضير الباك الحر؟

هل تحتاج الى طريقة لتنظيم وقتك و عمل برنامج مراجعة جيد للرياضيات و في حساب و تأويل النهايات ؟

ادخل اسمك و ايميلك هنا و التحق بأكثر من 52431 مترشح يستفيدون الان