حساب التكامل – ملخص المكاملة بالاجزاء + قاعدة التكامل بالاجزاء – الدرس 2 –

مرحبا بك في عالم المكاملة بالاجزاء، و حساب التكامل الصحيح. سوف نتطرق هنا بالتفصيل لكيفية حساب المكاملة بالاجزاء من الصفر و بالتفصيل. لكي تفهم جيدا هذه القاعدة. لكن قبل ذلك سوف نتعرف على تقنية حساب مساحة الحيز المحصور بين دالة و محور الافاصيل، أو كما نسميها ايضا حساب المساحة بالتكامل.

ثم سنختم بمثالين مفصلين خطوة بخطوة لكي تتدرب على حساب التكامل بالأجزاء.

الفيديوات بالعربية في الاسفل !!

لمتابعة الفيديوات اللاحقة، اضغط على السهم الاخضر أسفله

ملاحظة : في هذا الدرس يوجد جزء مخصص لأصحاب العلوم الرياضية … و لكن بالنسبة للأشخاص اللذين يريد الذهاب بعيدا في دراستهم، ، يستهدفون كلية الطب أو المدارس العليا يمكنهم متابعتها، فالامر ليس صعب.

الفيديو الأول : تقنية حساب مساحة الحيز المحصور بين دالة و محور الافاصيل باستعمال حساب التكامل

الدقيقة  00:00 : نتابع هنا المثال التطبيقي المتعلق بحساب التكامل لنحدد القيمة المتوسطة لدالة في مجال.

الدقيقة 00:30 : التأويل الهندسي و حساب التكامل : لنأخذ مثالا توضيحيا سهلا. اذا أخذنا دالة متصلة و موجبة.

فيمكننا الربط بين حساب التكامل على مجال [a,b] و التأويل الهندسي للمساحة المخططة المحصورة في الصورة.

من خلال خاصية مساحة الحيز التكامل يمثل المساحة التي توجد بين محور الأفاصيل و منحنى الدالة f بين النقطتين a و b.

أو بصيغة أخرى نقول أنه اذا كانت f متصلة و موجبة على المجال [a,b]

فان مساحة الحيز المحصور بين Cf و محور الأفاصيل و المستقيمين x =a و x = b هو المساحة A و التي يتم تحديدها بحساب تكامل الدالة f من a الى b.

الدقيقة 04:18 : لنبدأ بمثال توضيحي سهل لحساب المساحة بالتكامل ونأخذ الدالة

f(x)=x^2 بين النقطتين x=1 و x = 2 .

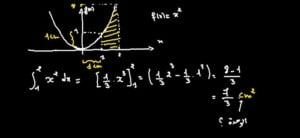
نستنتج إذن أن التأويل الهندسي للتكامل المحسوب هو بالضبط مساحة الحيز المحصور بين 1 و 2 و بين منحنى F و محور الافاصيل

الدقيقة 07:13 : كيفية تحديد الوحدات التي يجب استخدامها في حساب المساحات في التكامل ؟ 

الدقيقة 09:40 : ما هي الطرق الصحيحة لحساب التكامل :

• استعمال مباشر لعلاقات الدالة الأصلية.
• استعمال طريقة التكامل بالاجزاء.
• التكامل بتغيير المتغير : خاص بالعلوم الرياضية.

الدقيقة 11:15 : بما أننا تكلمنا سابقا عن علاقات الدالة الاصلية، لنمر مباشرة الى التكامل بالأجزاء – أو المكاملة بالأجزاء –

هذه هي العلاقة الرئيسية التي يجب أن تفهمها ثم تحفضها : U و V متصلتان على I , و a و b عنصران من I .

الدقيقة 13:13 : أمثلة لحساب التكامل بطريقة المكاملة بالأجزاء.

الفيديو الثاني : المكاملة بالاجزاء تمارين تطبيقية

الدقيقة 00:00 : نبدأ تطبيقنا للمكاملة بالاجزاء بمثال سهل

احسب التكامل التالي للدالة x*exp(x) بين 0 و 1

هنا يجب أن تنتبه لهذا الخطأ القاتل في حساب التكامل

الخطأ: تكامل جداء دالتين لا يساوي جداء تكامل كل دالة لوحدها

خطأ شائع عند المترشحين و يخرج على الكثيرين في الامتحان الوطني. فانتبه له جدا جدا!

هنا لحساب هذا التكامل نحن نحتاج أن نستعمل طريقة المكاملة بالأجزاء.

كيف نفعل ذلك؟

الخطوة 1: نحدد بدقة ماهي الدالة ‘u ؟

الخطوة 2: ثم نحدد ما هي الدالة v؟

الخطوة 3 : ثم أمامهما نحسب الدالة الاصلية ل u. و نحسب المشتقة v’.

الخطوة 4: نطبق علاقة المكاملة بالاجزاء مباشرة كما تعمناها أعلاه.

بهذه الطريقة نضمن أن لا نقوم بأغلاط في حساب المكاملة بالاجزاء.

الدقيقة 04:17 : جيد! أنت تعمل بجد معي!

نمر معا الى مثال ثاني تطبيقي حول حساب التكامل بالاجزاء لدالة جيبية تحتوي على ال sin(x)

نعيد الخطوات الاربعة بانتباه شديد.

ثم نطبق علاقة التكامل بالاجزاء

و voilà

ملاحظة أخيرة: أكبر غلط يواجه التلاميذ في حساب المكاملة بالاجزاء هو حساب تكامل الدالتين ثم حساب جدائهما كما وضحت لك.

اكتب هذا الغلط في ورقة مستقلة مع خريطتك الذهنية، لكي تتذكره و لا تقع فيه يوم الامتحان المهم.

هل تجد مشاكل في تحضير الباك الحر؟ هل تحتاج الى طريقة لتنظيم وقتك و عمل برنامج مراجعة جيد للرياضيات و حساب التكامل ؟

ادخل اسمك و ايميلك هنا و التحق بأكثر من 52431 مترشح يستفيدون الان