الفيديوات بالعربية في الاسفل !!
لمتابعة الفيديوات اللاحقة، اضغط على السهم الاخضر أسفله
نكملوا ما بقا والوااا
الفيديو الأول :
الدقيقة 00:00 : تتمة شرح الحالات النسبية لفلكة و مستوى و استعراض الحالات الثلاث الممكنة :
الحالة الأول : d(Omega , (P)) > R في هذه الحالة نقول أن الفلكة و المستوى لا يتقاطعان.
الحالة الثانية : d(Omega , (P)) = R في المستوى مماس للفلكة في نقطة وحيدة , و كأن الفلكة موضوعة فوق المستوى , مثل كرة تنس على الطاولة.
الحالة الثالثة : d(Omega , (P)) < R في هذه الحالة المستوى و الفلكة يتقاطعان وفق دائرة.
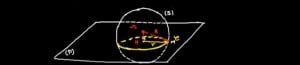
الدقيقة 06:00 : في حالة تقاطع الفلكة و مستوى حسب دائرة فان :

كما تبين الصورة فان :
R : شعاع الفلكة S.
r : شعاع الدائرة.
d(Omega ; (P)) : OmégaH.
الدقيقة 12:36 : المثال الأول السهل الذي يبين دراسة الحالات النسبية لمستوى و فلكة.
الفيديو الثاني :
الدقيقة 00:00 : تتمة المثال الأول التي ستمثل في دراسة تقاطع الفلكة S التي مركزها (Omega ( 1,2,3 و شعاعاها 4. و المستويات :
المستوى () : x +2y +2z +1=0
المستوى () : 2x – y + 2z +2=0
المستوى () :3x +2y -racine(3)z+1
حيث أن المرحلة الأولى تتمثل في حساب المسافة بين مركز الفلكة و المستويات الثلاث .
الدقيقة 02:22 : ايجاد المسافة بين المستوى الأول و مركز الفلكة و الذي حصلنا فيه على أن المسافة تساوي الشعاع و بالتالي فان المستوى الأول مماس للفلكة S.
الدقيقة 03:36 : بداية حساب المسافة بين مركز الفلكة و المستوى الثاني .
الدقيقة 07:16 : ايجاد أن المستوى الثاني يتقاطع مع الفلكة في دائرة.
الدقيقة 07:59 : استعمال علاقة شعاع الدائرة الناتجة عن تقاطع مستوى و فلكة.










