ملخص قواعد الدالة الأسية + اشتقاق الدالة الاسية + ملخص قواعد النهايات exp الدرس1 –

الفيديوات بالعربية في الاسفل !!

لمتابعة الفيديوات اللاحقة، اضغط على السهم الاخضر أسفله

في هذا الدرس سنتناول قواعد exp ، أو قواعد الدالة الاسية بالتفصيل. هذه الدوال الأسية من بين الدروس المهمة في الرياضيات بعد الدوال اللوغارتمية و التي سنستخدمها أيضا في الفيزياء.

فاذا كنت من الأشخاص الذين يحبون الرياضيات فعلى الأرجح يجب ان تتعمق في  درس exp. لماذا؟ فيه نقط جيدة في الوطني، و يمكن أن يرفع نقطتك و معدلك كثيرا! 

و لا تنسى أنه من الدروس الأكثر  متعة في الرياضيات.

قواعد الدالة الاسية أو قواعد exp

الفيديو الأول لقواعد exp

الدقيقة  00:00 : مثال أول سهل تعريف الدالة الأسية و التي سيمكننا من التعرف على قواعد الدالة exp الأساسية:

(f(x)=exp(x

مجال تعريف الدالة الأسية exp هو Df =R

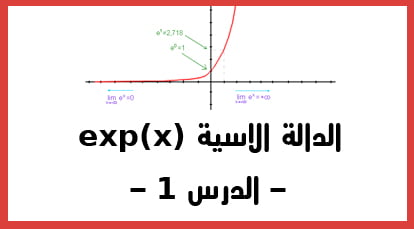
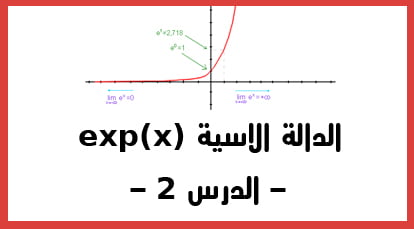
الدقيقة 01:09 : الرسم المبياني للدالة الاسية exp. حيث أن هذا التمثيل يقطع محور الأراتب في النقطة 1 و منه نستنتج بعض قواعد exp.

مثلا نستنتج أن exp(0)=1 و exp(1)= e =2.71.

الدقيقة03:40 : انطلاقا من الرسم المبياني للدالة يتبين لنا أن الدالة الأسية دائما أكبر من الصفر. إذن نستنتج القاعدة الثانية ل الدالة  exp الأسية هي أنها دالة موجبة على مجال تعريفها.

 و نكتب هذه القاعدة المهمة هكذا exp(x)>0 مهما يكن x ينتمي الى R.

الدقيقة 03:53 : مثال بسيط على موجبية الدالة الأسية.

الدقيقة 05:15 : نتابع قواعد الدالة الأسية : exp هي دالة تزايدية قطعا على مجال تعريفها.

الدقيقة 05:55 : نهاية الدالة الأسية exp عندما يؤول x الى مالانهاية هي مالانهاية.

النهايات الاعتيادية ل exp  للدالة الاسية

الدقيقة 07:22 : النهايات الاعتيادية ل exp  للدالة الأسية التي يجب معرفتها

سجلها عندك و ركز عليها.

افهم جيدا أن قواعد النهايات exp هذه هي محور الاسئلة التي تجدها في الامتحانات، بمعنى، أنه يجب عليك تغيير كتابة النهايات المطلوية في التمارين، لتكتبها على هذا شكل هذه القواعد النهايات exp. 

ثم بعد ذلك تقول : هذه النهاية اعتيادية ل exp و قيمتها هي 0 مثلا

و منه نستنتج …

اشتقاق الدالة الاسية – اشتقاق exp

نمر الى جزء مهم في درس exp هو كيفية اشتقاق exp بطريقة صحيحة. 

هذا يطرح مشكلا كبيرا للتلاميذ في الامتحانات. لماذا؟

لأن اشتقاق exp غريب نوعا ما.

الدقيقة 09:12 : الدالة المشتقة للدالة الأسية حيث أن exp(x)’=exp(x)  أي أن اشتقاق الدالة الأسية هي نفسها

يبدو الامر سهلا. لكن يتعقد عندما تكون هناك دالة داخل الاس

مثلا F(x)= exp(3x+4)

في هذه الحالة قواعد اشتقاق exp تخبرنا أن 

F(x)= exp(3x+4)=(3x+4)’*exp(3x+4)=3*exp(3x+4)

بمعنى أن اشتقاق الدالة الاسية الصحيح يتطلب اشتقاق ما يوجد بين قوسين exp 

ثم نضرب هذا الاشتقاق في الدالة الاسية الاولى.

انصحك مثلا بحساب مشتقات هذه الدوال لتفهم قواعد اشتقاق exp فهما جيدا:

F(x)= exp(3x^2+4x)

F(x)= exp(5x^4+4x^2+4)

F(x)= exp(3x+1/x)

F(x)= exp( sin(x)+4x )

الدقيقة 01:05 : مثال سهل مفصل حول اشتقاق الدالة الاسية :

(f(x)=3x + exp(x

(f'(x)= x +exp(x

لكنك قد تتسائل ماهي قاعدة اشتقاق exp بصفة عامة؟

مرحبا خذها و اكتبها و احفظها … و أكثر أهمية طبقها على الاقل خمسة مرات 

إذا لاحظت جيدا فاشتقاق الدالة الاسية، هو حالة خاصة من اشتقاق مركب دالتين.

بمعنى أن الاشتقاق الصحيح ل exp يخرج اشتقاق الدالة الداخلية u ثم يضربها في الدالة الاسية exp(u)

أنا أوكد كثيرا هنا على حساب الاشتقاق … لأن أي غلط في حساب اشتقاق الدالة الاسية exp في امتحان سوف يضيع نقطا كثيرة في الوطني. فانتبه جيدا!

الفيديو الثاني :

الدقيقة 00:00 : تابع في الفيديو مثال  آخر اصعب حول  اشتقاق الدالة الاسية.

تمرين لك: حاول أن تحسب هذه اشتقاق هذه الدالة الاسية في الوسخ، قبل أن ترى الحل!

الدقيقة  02:14 : خاصيات أساسية :

• exp(a+b)=exp(a)*exp(b) ة هذا شبيه بدرس القوى.
• exp(a-b)=exp(a)/exp(b)
• exp(-a)=1/exp(a)
• حالة الدالة الأسية الشبيهة بقوة قوة.

من هنا يتبين أن خاصيات القوى هي نفسها خاصيات الدوال الأسية.

الدقيقة 05:38 : الخاصيات التي سيتم استعمالها في حل المعادلات و المتراجحات التي تحتوي على الدالة الأسية.

• في حالة exp(a)=exp(b) <=> a =b
  • في حالة exp(a)<exp(b) <=> a <b

الدقيقة : مثال سهل لمتراجحة تحتوي على الدالة الأسية :

exp(3x+4)=1 <=> exp(3x+4)=exp(0)

<=> 3x+4=0 <=> x=-4/3

الدقيقة 08:20 : مثال اخر سهل لمتراجحة تحتوي على الدالة الأسية.

هل تجد مشاكل في تحضير الباك الحر؟ هل تحتاج الى ملخصات مركزة في جميع المواد + طريقة لتنظيم وقتك و عمل برنامج مراجعة للرياضيات و exp ؟

ادخل اسمك و ايميلك هنا و التحق بأكثر من 52431 مترشح يستفيدون الان