الفيديوات بالعربية في الاسفل !!
لمتابعة الفيديوات اللاحقة، اضغط على السهم الاخضر أسفله
الفيديو الأول :
الدقيقة 00:00 : المثال الأول السهل الذي يشرح الحالات النسبية لمستقيم و مستوى , حيث أن المستوى معرف بمعادلة ديكارتية (P) و مستقيمين (D) و (Delta) معرفان بمعادلة بارامترية. حيث أن السؤال هو هل المستقيم (D) عمودي على المستوى (P) أو هل المستقيم (Delta) عمودي على (P).
الدقيقة 20:4 : تحديد المعادلة الموجهة لكل مستقيم و التي احداثياتها هي العوامل المضروبة في t.
الدقيقة 04:38 : كيفية تحديد المتجهة المنظمية على المستوى (P) ؟ : يمكن حسابها بالمعاملات المضروبة في x في المعادلة الديكارتية للمستوى.
الدقيقة 06:00 : مقارنة احداثيات المتجهة المنظمية على المستوى (P) و المتجهة الموجهة لكل مستقيم على حدة من أجل ايجاد العلاقة بينها , حيث أن في هذه الحالة : u=2n .
الدقيقة 07:41 : كيفية استنتاج علاقة التعامد بين مستقيم و مستوى ؟
الدقيقة 08:53 : كيف نبين أن متجهتان غير متوازيتان ؟ : يتم ذلك عن طريق حساب مميز المتجهتين , و اذا وجدناه يخالف الصفر نستنتج أن المتجهتان غير مستقيميتان.
الفيديو الثاني :
الدقيقة 00:00 : تتمة الشرح و استنتاج الحالات النسبية لمستقيم و مستوى.
الدقيقة 00:54 : كيفية تحديد تعامد مستويين ؟
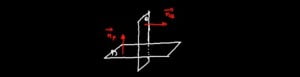
من خلال الشكل يتبين أنه من أجل أن نبين أن المستويين (P) و (Q) متعامدان يكفي أن نبين أن المجهتان المنظميتان متعامدتان.
الدقيقة 04:35 : مثال أول سهل حول تعامد مستويين :
نعتبر المستويات :
P) : 2x +3y + 4z +5 =0)
Q) : -3x +2y +7 =0)
Q’) : x + y + z -2 =0)
هل المستوى (P) عمودي على المستوى (Q) ؟
و هل المستوى (P) عمودي على المستوى (‘Q) ؟
الدقيقة 06:40 : ايجاد المتجهات المنظمية على كل مستوى.
الدقيقة 09:30 :
الدقيقة : كيف نبين أن متجهة عمودية على أخرى من أجل تبيان تعامد مستويين ؟ : من أجل القيام بذلك نحسب الجداء السلمي للمتجهتين.










