و نكمل مع مبرهنة التقابل ……
الفيديو الأول :
الدقيقة 00:00 : التمثيل الهندسي لمبرهنة التقابل و ذلك بعد تمثيل شرط الرتابة :
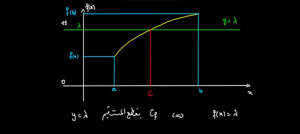
الدقيقة 04:38 : المثال الأول التطبيقي السهل حول تطبيق مبرهنة التقابل و ذلك بعد تبيان شرط الاتصال و شرط الرتاية.
الدقيقة 06:55 : كيفية دراسة رتابة دالة و دراسة رتابتها في مجال تعريفها ؟ : يتم ذلك عن طريق دراسة اشارة مشتقة الدالة و تمثيل جدول التغيرات أو دراستها جبريا.
الدقيقة 11:11 : استنتاج رتابة الدالة f.
الدقيقة 12:50 : حساب النهايات في محدات مجال تعريف الدالة من أجل تبيان الشرط الثالث من شروط تطبيق مبرهنة التقابل.
الفيديو الثاني :
الدقيقة 00:00 : تتمة حساب النهايات في محدات الدالة f.
الدقيقة 01:50 : برهنة شرط الاتصال و استعراض شرط الرتابة و شرط المقارنة من أجل تطبيق مبرهنة التقابل و حل المعادلة f(x)=0 التي تقبل حلا وحيدا.
الدقيقة 08:49 : كيف نحسب أو نؤطر حل معادلة على شكل f(x)=lamda ؟ في هذه الحالة نستخدم طريقة تسمى بطريقة التفرع الثنائي و ذلك بالطريقة التالية :
- نحدد مجال بدئي [a0,b0] بحيث c ينتمي الى هذا المجال.
- تقسيم هذا المجال الى نصفين.
- حساب سعة المجال.
- نعيد المرحلتين 2 و 3 حتى نصل الى السعة المنشودة.
الدقيقة 14:30 : تطبيق طريقة التفرع الثنائي – بداية الشرح –




merci prof kolxi super