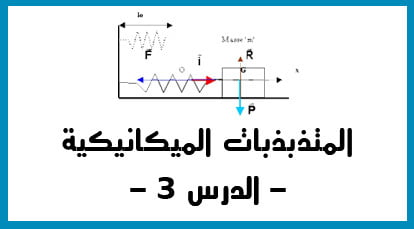
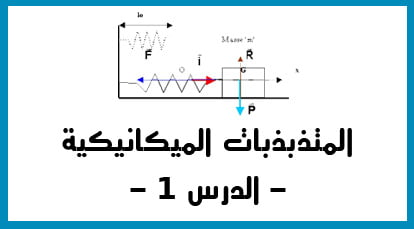
و نكمل مع المعادلات التفاضلية للنواسات …..
الفيديو الأول :
الدقيقة 00:00 : حساب الدالة المشتقة لمعادلة الطاقة الحركية – باستعمال خاصيات الاشتقاق – من أجل الحصول على المعادلة التفاضلية.
الدقيقة 07:30 : استنتاج أن طريقتي ايجاد المعادلة التفاضلية و اللتان تتمثلان في طريقة الطاقة الميكانيكية و طريقة العلاقة العامة للديناميك تؤديان الى نفس النتيجة .
الدقيقة 08:14 : كيف يتمكن تحديد المعادلة التفاضلية في حالة التذبذبات الصغيرة ؟ : اذا كانت التذبذبات صغيرة بحيث زاوية التذبذبات تكون أصغر من 15 درجة فاننا نأخد sin(theta ) = theta.
الدقيقة 09:48 : المعادلة التفاضلية الاجمالية للنواس البسيط :
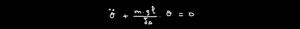
الدقيقة 11:20 : تحديد حل المعادلة التفاضلية للنواس :
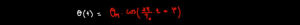
الدقيقة 12:48 : كيفية تحديد و رسم التذبذبات و الطور عند أصل التواريخ و ذلك باستخدام الشروط البدئية ؟
الفيديو الثاني :
الدقيقة 00:00 : ما هو نواس اللي ؟ : نواس اللي هو عبارة عن نواس فولاذي اسطواني ثابتته c , محوره رأسي مثبث أعلاه بحامل و يحمل في طرفه الأسفل قضيبا فلزيا أفقيا، و يكمنه الدوران حول محور.
الدقيقة 01:50 : كيف يتحرك نواس اللي ؟
نقوم بادارة القضيب الفلزي عن موضع توازنه ثم نحرره فيقوم بحركة تذبذبية و في هذه الحالة تكون الاحتكاكات مهملة.
الدقيقة 04:37 : ما هو الجسم المدروس في حالة نواس اللي ؟ : الجسم المدروس هو السلك.
الدقيقة 05:18 : تحديد محور الدوران اضافة الى جرد العزوم المطبقة على السلك.
الدقيقة 07:20 : تطبيق العلاقة الأساسية للديناميك على السلك من أجل تحديد المعادلة التفاضلية اضافة الى تحديد القوى التي يكوت عزومها منعدما.
الدقيقة 12:00 : تحديد حل المعادلة التفاضلية التي تعتير معادلة من الدرجة الثانية.
الدقيقة 13:36 : تحديد الثوابت التالية : حساب وسع التذبذبات و الطور باستعمال الشروط البدئية.