الفيديو الأول :
الدقيقة 00:00 : تتمة شرح تحديد قيمة التوتر بدلالة الزمن اضافة الى تحديد قيمة طور التوتر بالنسية للتيار و حيث من الممكن تحديده سواءا مبيانيا أو بطريقة الممانعة.
الدقيقة 02:37 : كيفية تحديد المعادلة التفاضلية بالنسبة للدارة + التمثيل المبياني للدارة RLC , و التي نستخدمها من أجل تمثبل توتر المقاومة و الوشيعة و المكثف اضافة الى منحى التيار الكهربائي.
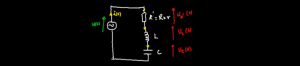
الدقيقة 04:20 : تطبيق قانون تجميعية التوترات من أجل تحديد المعادلة التفاضلية للدارة.
الدقيقة 06:12 : كيفية استخدام تعبير الوشيعة في قانون تجميعية التوترات من أجل ايجاد المعادلة التفاضلية.
الدقيقة 06:40 : استخدام علاقة التيار و التوثر بين مربط المكثف.
الدقيقة 08:36 : التعبير الاجمالي للمعادلة التفاضلية في حالة دارة RLC متوالية في تذبذبات جيبية.
الدقيقة 01:30 : كيف يمكن تحديد حل المعادلة التفاضلية من الدرجة الثانية في حالة التذبذبات القسرية ؟ : في هذا الدرس حل هذه المعادلة غير مطلوب فقط سنقوم بتحديدها مبيانبا.
الدقيقة 12:00 : الانتقال الى الفقرة الثالثة من الدرس و التي تخص تحديد المقادير بدلالة التردد N (بدلالة النبض).
الدقيقة 12:46 : التمثبل المبياني للدارة المتوالية RLC و التي سنستخدمها في دراسة التردد و ذلك بطريقة الممانعة – بداية الشرح –
الفيديو الثاني :
الدقيقة 00:00 : التمثبل المبياني للدارة المتوالية RLC و التي سنستخدمها في دراسة التردد و ذلك بطريقة الممانعة, اضافة الى التمثيل المبياني للدالة :
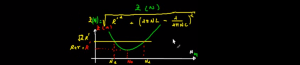
الدقيقة 02:39 : تحديد تعبير No التردد الخاص للدارة RLC , و الذي يعتبر مقدار مرتبط بمعامل التحريض L و بسعة المكثف.
الدقيقة 03:56 : تحديد تعبير التيار الفعال Ieff (القيمة الفعالة للتوثر) و التعرف على القيمة القصوى Io عند الرنين و التي نحصل عليها عند No :
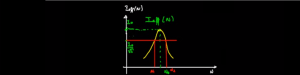
الدقيقة 07:17 : تحديد المنطقة الممررة في التمثيل الخاص بالممانعة و التمثيل الخاص بالتيار الفعال.
الدقيقة 08:50 : دراسة ظاهرة الرنين و التي تقع في حالة N=N0 .
الدقيقة 10:38: كيف يكون تعبير الممانعة في حالة الرنين ؟ : من خلال تعبير الممانعة في حالة الرنين نقول أنه في حالة الرنين تكون الممانعة دنوية و Z=Zmin = R +r.
الدقيقة 12:43: كيف يكون تعبير القدرة المتوسظة في حالة الرنين ؟ : في حالة الرنين تكون القدرة المتوسطة في حالة قصوية.
الدقيقة 13:11 : تحديد التمثيل المبياني لعلاقة القدرة المتوسطة بالتردد :






